
You can't travel anywhere without going over some kind of bridge. Bridges help to drastically reduce the travel time it would take to go around the hazard you are trying to go over. Bridges are a critical part of our country's infrastructure and must be protected to keep traffic moving efficiently.
Bridges are designed to handle traffic and the weight they carry. However, during the 1950's and 1960's trucks began to get significantly heavier and new protections had to be adopted to prevent damage to bridges. The solution was to tie allowable weights to the number and spacing of axles.
Axle spacing is as important to a bridge as the weight that is has to hold. If you imagine walking on snow, your feet go through the snow and hit the ground below. If you walk on the same snow with snow shoes, your weight is displaced around a greater area and this allows you to walk on top of the snow without going through it. This is the same concept used for the federal bridge law. The more distance there is between axles the lower the overall force that is applied to the bridge.
What is the bridge formula?
The bridge formula is a simple math formula that you can use to determine if you weigh is acceptable for crossing a bridge in the US. The federal bridge formula is:
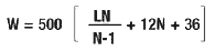
W = the maximum weight in pounds that can be carried on a group of two or more axles to the nearest 500 pounds.
L = the distance in feet between the outer axles of any two or more consecutive axles.
N = the number of axles being considered.
This formula limits the weight on groups of axles in order to reduce the risk of damage to highway bridges. Allowable weight depends on the number of axles a vehicle has and the distance between those axles. However, the single- or tandem-axle weight limits supersede the Bridge Formula limits for all axles not more than 96" apart.
Why is the bridge formula necessary?
The bridge formula is necessary because it helps to understand how much stress can be applied to a bridge without affecting the structural integrity. When the load is spread out across a longer distance the force applied to the bridge is lower. This can be seen in the figure below.
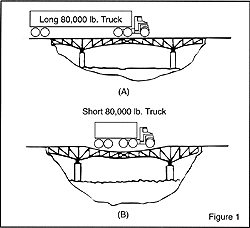
In example (B) you can see that a smaller truck with the same weight causes more pressure on the bridge which can reduce it's lifespan. This is the main reason why the federal bridge laws were formed. The cost fix and replace bridges can be a huge expense on a community requiring higher taxes. The Bridge law helps avoid this scenario by requiring trucks to limit the amount of weight and distance between axles.
How do you use the bridge formula?
The weight on various axle configurations must be checked to determine compliance with the Bridge Formula. Three definitions are needed to use the Bridge Formula correctly.
- Gross Weight—The weight of a vehicle or vehicle combination and any load thereon. The Federal gross weight limit on the Interstate System is 80,000 pounds unless the Bridge Formula dictates a lower weight limit.
- Single-Axle Weight—The total weight on one or more axles whose centers are spaced not more than 40 inches apart. The Federal single-axle weight limit on the Interstate System is 20,000 pounds.
- Tandem-Axle Weight—The total weight on two or more consecutive axles whose centers are spaced more than 40 inches apart but not more than 96 inches apart. The Federal tandem-axle weight limit on the Interstate System is 34,000 pounds.
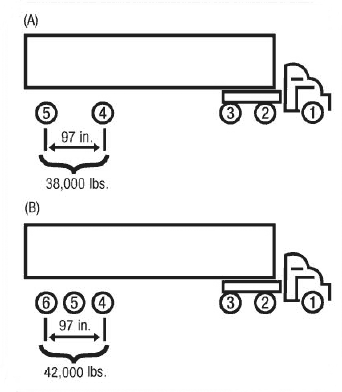
Bridge Formula calculations yield a series of weights. It is important to note that the single-axle weight limit replaces the Bridge Formula weight limit on axles not more than 40 inches apart, and the tandem-axle weight limit replaces the Bridge Formula weight limit for axles over 40 but not more than 96 inches apart. At 97 inches apart, for example, two axles may carry 38,000 pounds (A) and three axles may carry 42,000 pounds, as shown in (B).
The vehicle with weights and axle dimensions shown in the figure below is used to illustrate a Bridge Formula check.
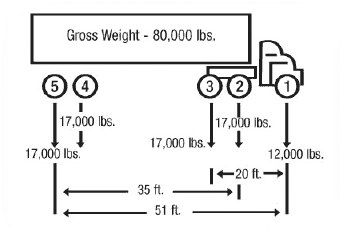
Before checking for compliance with the Bridge Formula, a vehicle's single-axle, tandem-axle, and gross weight should be checked. Here the single axle (number 1) does not exceed 20,000 pounds, tandems 2-3 and 4-5 do not exceed 34,000 pounds each, and the gross weight does not exceed 80,000 pounds. These preliminary requirements are satisfied. The first Bridge Formula combination is checked as follows:
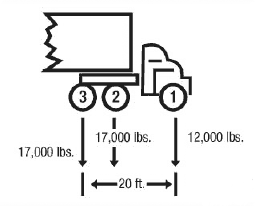
Figure 5
Check axles 1 through 3 (Figure 5)
Actual weight = 12,000 + 17,000 + 17,000 = 46,000 pounds.
N = 3 axles
L = 20 feet
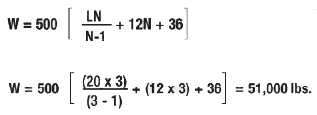
Maximum weight (W) = 51,000 pounds, which is more than the actual weight of 46,000 pounds. So, the Bridge Formula requirement is satisfied.
Example From the Bridge Table
This same number (51,000 pounds) could have been obtained from the Bridge Table by reading down the left side to L = 20 and across to the right where N = 3.
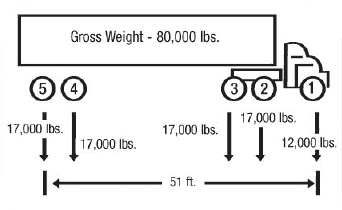
Figure 6
Now check axles 1 through 5 (Figure 6)
Actual weight = 12,000 + 17,000 + 17,000 + 17,000 + 17,000 = 80,000 pounds.
Maximum weight (W) = 80,000 pounds (Bridge Table for "L" of 51 feet and "N" of 5 axles).
Therefore, this axle spacing is satisfactory.
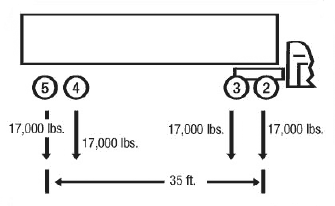
Figure 7
Now check axles 2 through 5 (Figure 7)
Actual weight = 17,000 + 17,000 + 17,000 + 17,000 = 68,000 pounds.
Maximum weight (W) = 65,500 pounds (Bridge Table for "L" of 35 feet and "N" of 4 axles).
This is a violation because the actual weight exceeds the weight allowed by the Bridge Formula. To correct the situation, some load must be removed from the vehicle or the axle spacing (35 feet) must be increased.
Exception to Formula and Bridge Formula Table
In addition to the grandfather rights notes on page 3, Federal law (23 U.S.C. 127) includes one other exception to the Bridge Formula and the Bridge Table—two consecutive sets of tandem axles may carry 34,000 pounds each if the overall distance between the first and last axles of these tandems is 36 feet or more. For example, a five-axle tractor-semitrailer combination may carry 34,000 pounds both on the tractor tandem (axles 2 and 3) and the trailer tandem (axles 4 and 5), provided axles 2 and 5 are spaced at least 36 feet apart. Without this exception, the Bridge Formula would allow an actual weight of only 66,000 to 67,500 pounds on tandems spaced 36 to 38 feet apart.
Bridge Formula Application to Single-Unit Trucks
The procedure described above could be used to check any axle combinations, but several closely spaced axles usually produce the most critical situation.
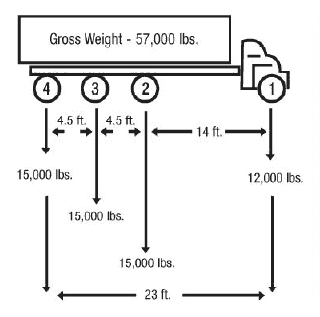
Figure 8
The truck shown in Figure 8 satisfies the single-axle weight limit (12,000 pounds are less than 20,000 pounds), the tandem-axle limit (30,000 pounds are less than 34,000 pounds) and the gross-weight limit (57,000 pounds are less than 80,000 pounds). With these restrictions satisfied, a check is done for Bridge Formula requirements, axles 1 through 4.
Actual weight = 12,000 + 15,000 + 15,000 + 15,000 = 57,000 pounds.
Maximum weight (W) = 57,500 pounds (Bridge Table for "L" of 23 feet and "N" of 4 axles).
Since axles 1 through 4 are satisfactory, check axles 2 through 4:
Actual weight = 15,000 + 15,000 + 15,000 = 45,000 pounds.
Maximum weight (W) = 42,500 pounds (Bridge Table for "L" of 9 feet and "N" of 3 axles.
This is a violation because the actual weight exceeds the weight allowed by the Bridge Formula. The load must either be reduced, axles added, or spacing increased to comply with the Bridge Formula.
What happens if I violate the bridge law?
Each state is responsible for it's own enforcement and collection of fines so penalties will vary. If you are found to be heavy on an axle or in violation of the federal bridge law it is likely this will impact your CSA score. Overweight axles fall under the FMCSA's unsafe driving BASIC.
To avoid violating bridge laws it is always a good idea to plan you route ahead and use an onboard truck scale solution to know what your axle weights are during loading. If you are going to be considered overloaded in a state and cannot adjust your 5th wheel or trailer tandem axles to remain legal then you can obtain an overweight permit.
If you were found to be in violation in error by the DOT you can file a DataQ with the FMCSA to appeal the violation and have it removed.
Bridge Weight Reference Table
|
Length |
2 Axles |
3 Axles | 4 Axles | 5 Axles | 6 Axles | 7 Axles | 8 Axles | 9 Axles |
| 4 | 34,000 | |||||||
| 5 | 34,000 | |||||||
| 6 | 34,000 | |||||||
| 7 | 34,000 | |||||||
| 8 & less | 34,000 | 34,000 | ||||||
| more than 8 | 38,000 | 42,000 | ||||||
| 9 | 39,000 | 42,500 | ||||||
| 10 | 40,000 | 43,500 | ||||||
| 11 | 44,000 | |||||||
| 12 | 45,000 | 50,000 | ||||||
| 13 | 45,500 | 50,500 | ||||||
| 14 | 46,500 | 51,500 | ||||||
| 15 | 47,000 | 52,000 | ||||||
| 16 | 48,000 | 52,500 | 58,000 | |||||
| 17 | 48,500 | 53,500 | 58,500 | |||||
| 18 | 49,500 | 54,000 | 59,000 | |||||
| 19 | 50,000 | 54,500 | 60,000 | |||||
| 20 | 51,000 | 55,500 | 60,500 | 66,000 | ||||
| 21 | 51,500 | 56,000 | 61,000 | 66,500 | ||||
| 22 | 52,500 | 56,500 | 61,500 | 67,000 | ||||
| 23 | 53,000 | 57,500 | 62,500 | 68,000 | ||||
| 24 | 54,000 | 58,000 | 63,000 | 68,500 | 74,000 | |||
| 25 | 54,500 | 58,500 | 63,500 | 69,000 | 74,500 | |||
| 26 | 55,500 | 59,500 | 64,000 | 69,500 | 75,000 | |||
| 27 | 56,000 | 60,000 | 65,000 | 70,000 | 75,500 | |||
| 28 | 57,000 | 60,500 | 65,500 | 71,000 | 76,500 | 82,000 | ||
| 29 | 57,500 | 61,500 | 66,000 | 71,500 | 77,000 | 82,500 | ||
| 30 | 58,500 | 62,000 | 66,500 | 72,000 | 77,500 | 83,000 | ||
| 31 | 59,000 | 62,500 | 67,500 | 72,500 | 78,000 | 83,500 | ||
| 32 | 60,000 | 63,500 | 68,000 | 73,000 | 78,500 | 84,500 | 90,000 | |
| 33 | 64,000 | 68,500 | 74,000 | 79,000 | 85,000 | 90,500 | ||
| 34 | 64,500 | 69,000 | 74,500 | 80,000 | 85,500 | 91,000 | ||
| 35 | 65,500 | 70,000 | 75,000 | 80,500 | 86,000 | 91,500 | ||
| 36 | 66,000 | 70,500 | 75,500 | 81,000 | 86,500 | 92,000 | ||
| 37 | 66,500 | 71,000 | 76,000 | 81,500 | 87,000 | 93,000 | ||
| 38 | 67,500 | 71,500 | 77,000 | 82,000 | 87,500 | 93,500 | ||
| 39 | 68,000 | 72,500 | 77,500 | 82,500 | 88,500 | 94,000 | ||
| 40 | 68,500 | 73,000 | 78,000 | 83,500 | 89,000 | 94,500 | ||
| 41 | 69,500 | 73,500 | 78,500 | 84,000 | 89,500 | 95,000 | ||
| 42 | 70,000 | 74,000 | 79,000 | 84,500 | 90,000 | 95,500 | ||
| 43 | 70,500 | 75,000 | 80,000 | 85,000 | 90,500 | 96,000 | ||
| 44 | 71,500 | 75,500 | 80,500 | 85,500 | 91,000 | 96,500 | ||
| 45 | 72,000 | 76,000 | 81,000 | 86,000 | 91,500 | 97,500 | ||
| 46 | 72,500 | 76,500 | 81,500 | 87,000 | 92,500 | 98,000 | ||
| 47 | 73,500 | 77,500 | 82,000 | 87,500 | 93,000 | 98,500 | ||
| 48 | 74,000 | 78,000 | 83,000 | 88,000 | 93,500 | 99,000 | ||
| 49 | 74,500 | 78,500 | 83,500 | 88,500 | 94,000 | 99,500 | ||
| 50 | 75,500 | 79,000 | 84,000 | 89,000 | 94,500 | 100,000 | ||
| 51 | 76,000 | 80,000 | 84,500 | 89,500 | 95,000 | 100,500 | ||
| 52 | 76,500 | 80,500 | 85,000 | 90,500 | 95,500 | 101,000 | ||
| 53 | 77,500 | 81,000 | 86,000 | 91,000 | 96,500 | 102,000 | ||
| 54 | 78,000 | 81,500 | 86,500 | 91,500 | 97,000 | 102,500 | ||
| 55 | 78,500 | 82,500 | 87,000 | 92,000 | 97,500 | 103,000 | ||
| 56 | 79,500 | 83,000 | 87,500 | 92,500 | 98,000 | 103,500 | ||
| 57 | 80,000 | 83,500 | 88,000 | 93,000 | 98,500 | 104,000 | ||
| 58 | 84,000 | 89,000 | 94,000 | 99,000 | 104,500 | |||
| 59 | 85,000 | 89,500 | 94,500 | 99,500 | 105,000 | |||
| 60 | 85,500 | 90,000 | 95,000 | 100,500 | 105,500 |

